Arthur's Blog

本文cmd地址：经典检索算法：BM25原理

bm25 是什么？

bm25 是一种用来评价搜索词和文档之间相关性的算法，它是一种基于概率检索模型提出的算法，再用简单的话来描述下bm25算法：我们有一个query和一批文档Ds，现在要计算query和每篇文档D之间的相关性分数，我们的做法是，先对query进行切分，得到单词$q_i$，然后单词的分数由3部分组成：

• 单词$q_i$和D之间的相关性
• 单词$q_i$和D之间的相关性
• 每个单词的权重

最后对于每个单词的分数我们做一个求和，就得到了query和文档之间的分数。

bm25 解释

讲bm25之前，我们要先介绍一些概念。

二值独立模型 BIM

BIM(binary independence model)是为了对文档和query相关性评价而提出的算法，BIM为了计算$P(R|d,q)$，引入了两个基本假设：

假设1
一篇文章在由特征表示的时候，只考虑词出现或者不出现，具体来说就是文档d在表示为向量$\vec x=(x_1,x_2,...,x_n)$，其中当词$t$出现在文档d时，$x_t=1$，否在$x_t=0$。
假设2
文档中词的出现与否是彼此独立的，数学上描述就是$P(D)=\sum_{i=0}^n P(x_i)$
有了这两个假设，我们来对文档和query相关性建模：

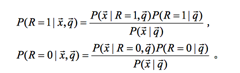
其中分别表示当返回一篇相关或不相关文档时文档表示为x的概率。

 

接着因为我们最终得到的是一个排序，所以，我们通过计算文档和query相关和不相关的比率，也可得文档的排序，有下面的公式：

 

其中是常数，我们可以不考虑，再根据之前的假设2：一个词的出现 与否与任意一个其他词的出现与否是互相独立的，我们可以化简上面的式子：

由于每个 xt 的取值要么为 0 要么为 1，所以，我们可得到：

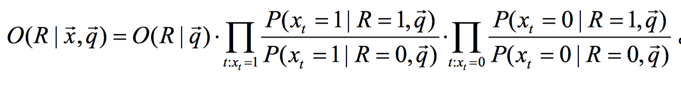
我们接着引入一些记号：
：词出现在相关文档的概率
：词出现在不相关文档的概率

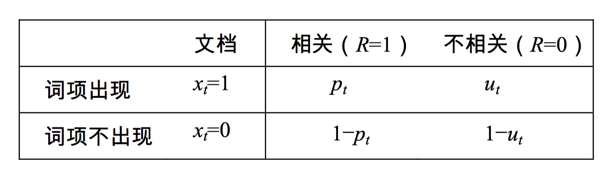
于是我们就可得到：

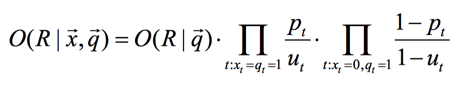
我们接着做下面的等价变换：

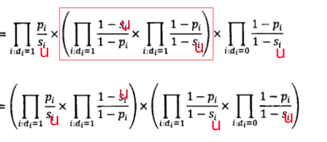
此时，公式中根据出现在文档中的词计算，则是所有词做计算，不需要考虑，此时我们定义RSV （retrieval status value），检索状态值：

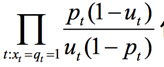
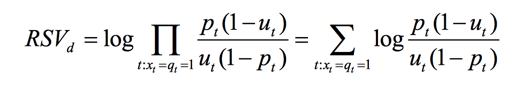
定义单个词的ct

下一步我们要解决的就是怎么去估计pt和ut，看下表：

其中dft是包含词t的文档总数，于是，
此时词t的ct值是：

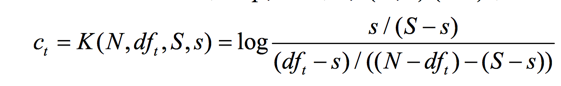
为了做平滑处理，我们都加上1/2，得到：